2.1. Convergence Test
Usually, a DP model is fitted to DFT data. The quality of the DFT dataset determines the accuracy limitation of the DP model. Ideally, we would like to generate DFT data as accurately as we can, e.g. using infinitely large ENCUT and infinitesimal KSPACING during DFT calculations. However, it is impossible in practice. We need to choose finite values for ENCUT and KSPACING. In addition, we need to achieve an acceptable trade-off between accuracy and efficiency. The ENCUT cannot be too large and the KSPACING cannot be too small. When training a DP model, tens of thousands of DFT single-point calculations would be carried out, which is very expansive meanwhile time-consuming. For example, assuming 10000 DFT calculations in total, 3 hours per calculation using nodes with 20 cores per-node, 600000 core*hours in total are needed. This is the reason why we encourage users to generate DFT data collaboratively. Therefore, to ensure the data quality, the reliability of the final model, as well as the feasibility of the project, a convergence test should be done first. Three goals are expected to achieve through the test:
to choose appropriate values of parameters in DFT calculations, such as ENCUT and KSPACING, ensuring that the DFT calculations are converged
to acquire an evaluation of the temporal and financial consumption of the project, which factor matters in designing the data generation scheme
to obtain a prior perception of error ranges as well as the intrinsic value of DFT energy, force, and stress (Virial), which are useful in setting pre-factors (and possibly fine-tune schemes) when training a DP model, as well as the configuration selection criteria in data generation scheme through DP-GEN
Special care should be taken that, 1) the convergence of three kinds of DFT labels (i.e. the energy, force, and Virial) are usually asynchronous, concerning the tightening up of calculation parameters 2) the convergence tendencies are configuration-dependent.
Before the test, convergence criteria for DFT results need to be clarified. Users are recommended to 1) make sure which labels are (more) important to the target properties or simulations in the project, 2) if attainable, map the expected accuracy of the targeted properties to the tolerances for specific labels (in specific configurations), 3) follow the general empirical convergence criteria, such as official recommendations from the developers of the adopted DFT code (could be reasonably overwritten by the specific requirement of the project).
Representive configurations are recommended to be used in convergence tests. A basic rule is to capture the maximum error fluctuation using configurations corresponding to extreme cases, i.e., to conduct a limit test. The cell_size/cell_shape/atom_perturbation… of the configuration should be customized according to the demands of the targeted properties.
For a simple example, when elastic properties are focused, the extreme cases in finite-difference calculations that provide the largest label_Virials (thus might also present the largest errors in Virials) may demand uniaxial compressions around +/-2% in longitude (norm deformation) or shear around +/-2% in cell_vector_projection (shear deformation). Consequently, 2% or more remarkably deformed configuration(s) might be good candidates to be tested.
Please note that the relation that extreme_deformation gives extreme_labels is case-specific, but configurations near equilibrium states would generally loosen the convergence condition where the intrinsic values of forces and Virials are close to zero. After making a successful compromise in calculation parameters, the third goal of the convergence test could also be considered.
for training scheme:
In DP, the loss function is: \(L(p_\epsilon,p_f,p_\xi)=p_\epsilon(\Delta\epsilon)^2+\frac{p_f}{3N}\sum_{i=1}^{N}\sum_{j=1}^{3}(\Delta F_{ij})^2+\frac{p_\xi}{9}\sum_{k=1}^{9}(\Delta \xi_k)^2\)
The first, second, and third part are corresponding to energy error, force error, and stress error (Virial error), respectively.
The facts are that different labels should physically be self-consistent as expected by the DP model in constructing the PES, and all (three) labels are counted in the loss function. However, three DFT labels are in practice obtained by different numerical methods relying on sophisticated artificial implementations that make their error ranges not self-consistent. Consequently, the accuracy in the focused label (according to the demands of the project) of the DP model could be sacrificed as the price in fitting the other labels with larger noises.
To avoid such unwanted cases, users could try adjusting the conservative weights in the loss function according to their needs and based on the result of the convergence test
Empirically, the error in Virials is the hardest to converge in most cases when using VASP and would influence the training accuracy and effectiveness in energy (training effectiveness, some cases need 10 times more training steps to achieve the same energy accuracy when using non-zero pref_V)
for data generation:
In DP-GEN, the configuration selection is implemented by the model deviation in forces (trust_f), thus the results in values of forces could help in setting the trust_f. Further details about model deviation and rules in setting trust_f please see related documents. Traditionally, convergence test in DFT calculations only tests on the total energy of an equilibrium cell, e.g. to obtain ENCUT and KSPACING values that achieve an error level in total energy less than 1 meV/atom. In comparison to traditional ways, there are two major differences to doing the convergence test here.
When generating a DFT dataset to train a DP model, we need to check the convergence of energy, force, and stress. Usually, the convergence criteria are set to 0.001. For energy and stress, 0.001 means the error is 0.001 eV/atom, while it is 0.001 eV/Å for the force. To transform a stress value into an energy value, the stress is multiplied by the volume of the simulation cell.
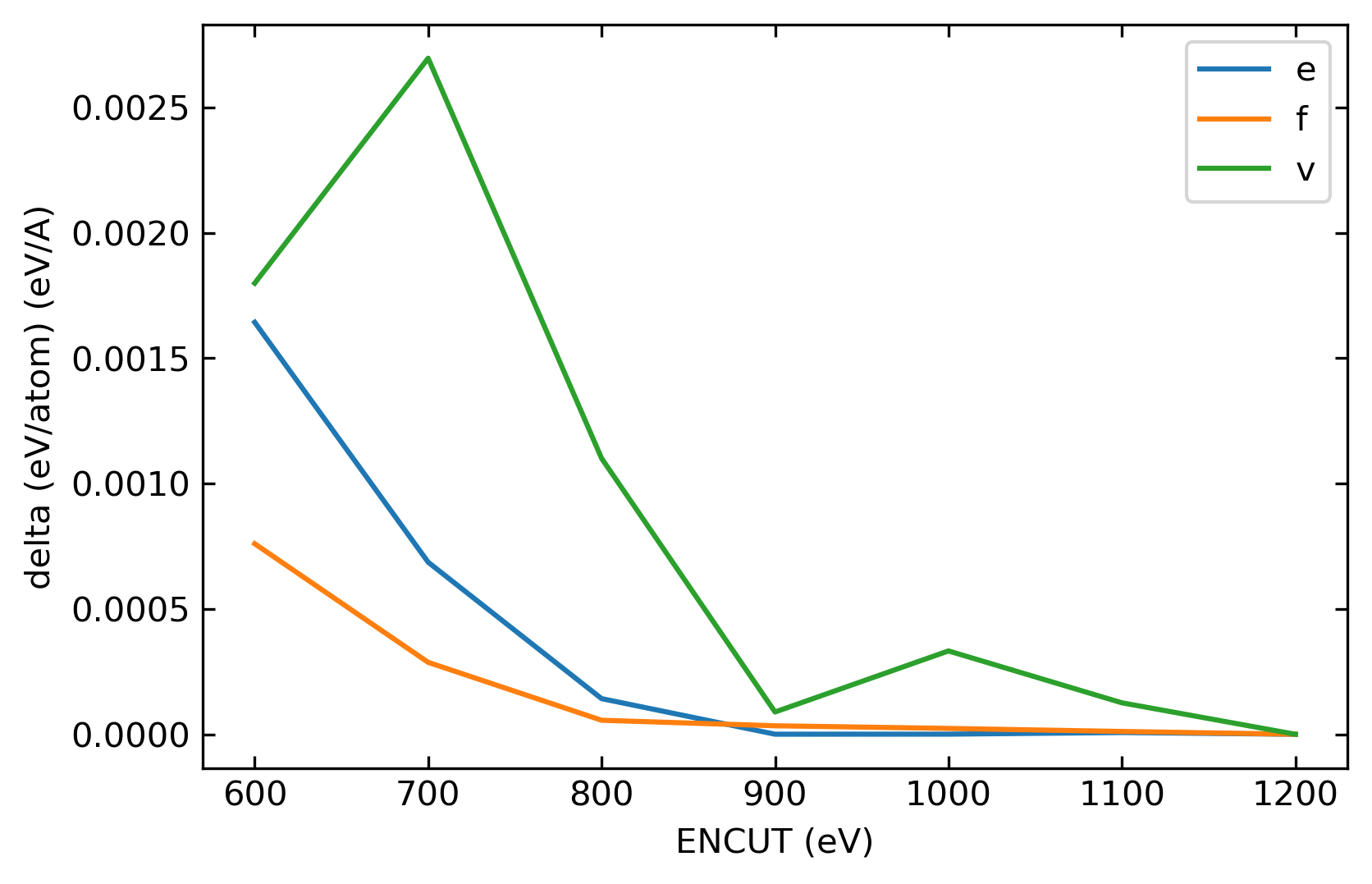
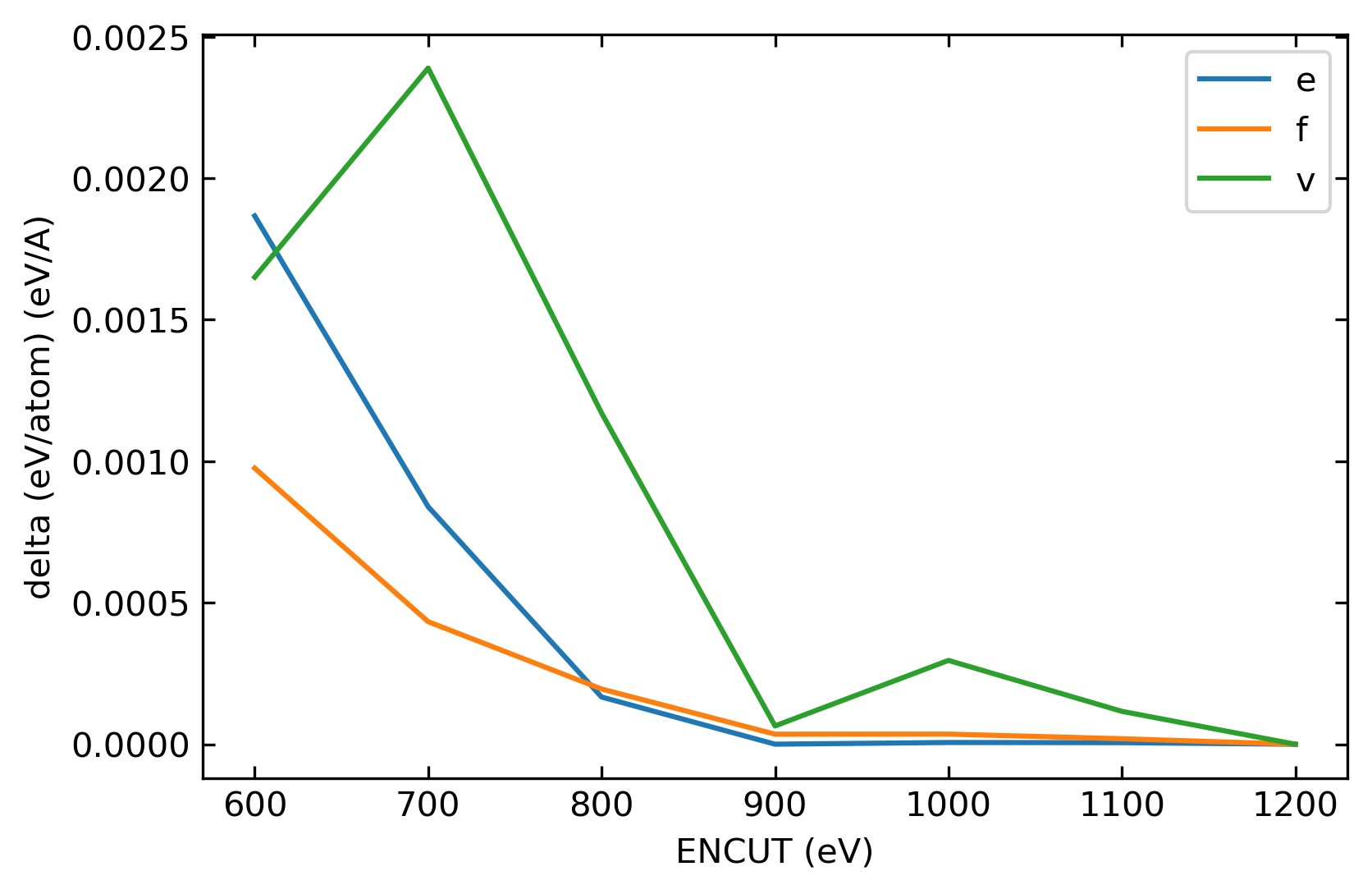
A highly distorted supercell instead of an undistorted unit cell close to equilibrium is always used in the convergence test. For example, for a solid phase, firstly expand the volume of an equilibrium supercell by ~5%; then randomly deform the supercell, e.g. with the strain components chosen as random values with an upper limit of 3%; and finally, randomly shift each atom by a random value (e.g. < 0.02 Å) in each dimension. Choosing a randomly distorted supercell to do a convergence test is because almost all the DFT samples are distorted supercells. Using an equilibrium undistorted unit cell usually overestimates the convergence level. During the convergence test of ENCUT, the value of KSPACING is fixed at a low value, e.g. 0.10 \(\rm{Å^{-1}}\). The variations of total energy (e), atomic force (f), and Virial (v) of a given configuration are calculated concerning the change of ENCUT. The following figure illustrates a typical example of how the total energy, atomic force, and Virial converge with ENCUT. In the figure, the values of ENCUT = 1200 eV are taken as references. ENCUT > 900 eV can meet our requirement when taking 0.001 as the criteria. The first one is the results of HfC, while the second one is the results of TaC.
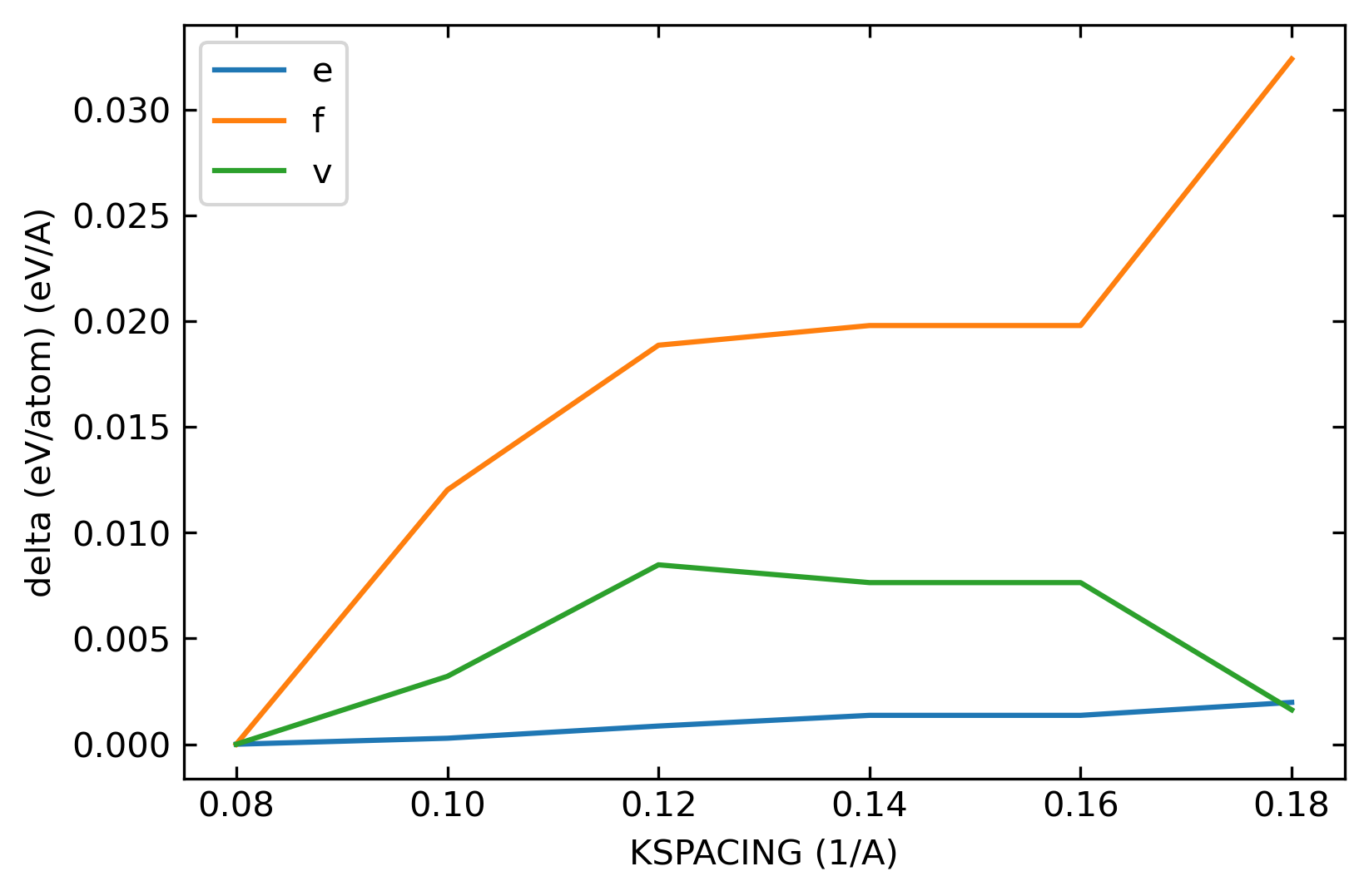
During the convergence test of KSPACING, the value of ENCUT is fixed at a high value, e.g. 1000 eV. The variations of total energy (e), atomic force (f), and Virial (v) of a given configuration are calculated with respect to the change of KSPACING. The following figure illustrates a typical example of how the total energy, atomic force, and Virial converge with KSPACING. In the figure, the values of KSPACING = 0.08 \(\rmÅ^{-1}\) are taken as references. Different from ENCUT, where good convergence tendency can be obtained, the convergence of force and Virial in KSPACING in this system is poor. It is possible that even the value of 0.08 \(\rmÅ^{-1}\) cannot reach the 0.001 criteria for force and Virial from this figure. Nevertheless, the energy convergence is good enough. All the KSPACING values may meet the 0.001 criteria. The first one is the results of HfC, while the second one is the results of TaC. 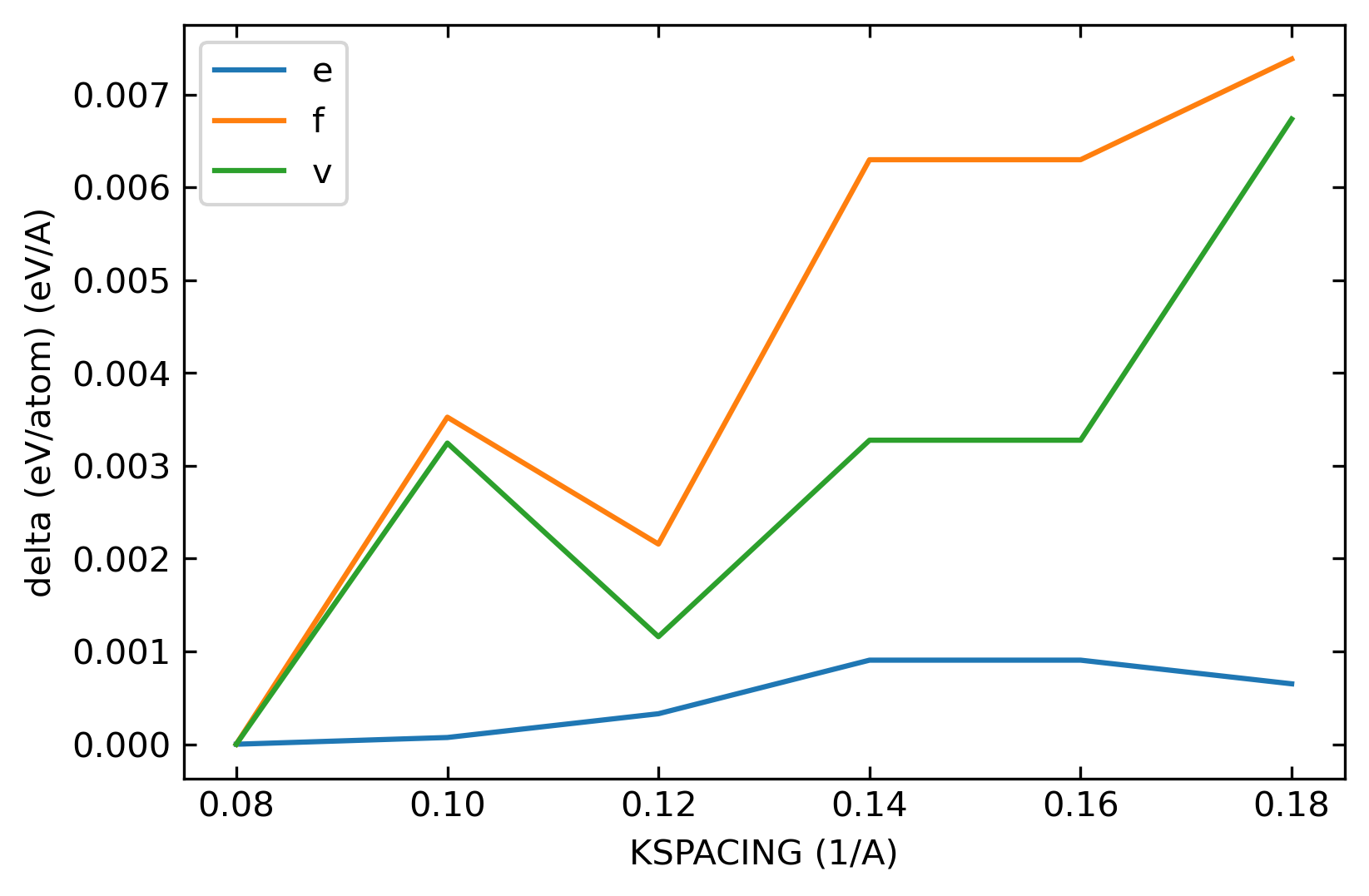
Overall, we can see that the accuracy of energy is the best among energy, atomic force, and Virial. In practice, the energy values are the most trustable. The accuracy of these arguments will influence the prediction accuracy of materials properties. For example, the following table shows the influence of convergence level on the prediction of properties. Since the energy converges well, the predictions on lattice parameters and cohesive energy are good, which do not vary significantly with KSPACING. However, the predictions on elastic constants depend strongly on the value of KSPACING, especially for TaC. As can be seen from the figure above, errors of TaC in force and stress are much higher than those of HfC. Therefore, the prediction accuracy of elastic constants of TaC is low. In practice, the smallest KSPACING value affordable is around 0.10 \(\rm{Å^{-1}}\), since we need to do tens of thousands of DFT calculations. Therefore, knowing the convergence level of your DFT calculations is essential, especially when we cannot reach the 0.001 criteria.
Compound | KSPACING(1/Å) | a(Å) | E/atom(eV/atom) | C11(GPa) | C12(GPa) | C44(GPa) |
|---|---|---|---|---|---|---|
HfC | 0.15 | 4.6467 | -10.5247 | 518.11 | 103.43 | 170.21 |
HfC | 0.10 | 4.6467 | -10.5247 | 519.44 | 102.12 | 175.52 |
HfC | 0.05 | 4.6470 | -10.5253 | 512.87 | 104.64 | 172.28 |
TaC | 0.15 | 4.4782 | -11.1065 | 590.20 | 193.68 | 171.34 |
TaC | 0.10 | 4.4782 | -11.1065 | 671.24 | 154.41 | 170.82 |
TaC | 0.05 | 4.4785 | -11.1039 | 708.46 | 134.13 | 175.99 |